





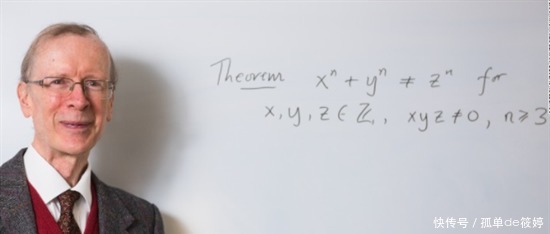

一个困惑了人类3个世纪的数学猜想,是怎样拯救
【作者】网站采编
【关键词】
【摘要】“将一个立方数分成两个立方数之和,或一个四次幂分成两个四次幂之和,或者一般地将一个高于二次的幂分成两个同次幂之和,这是不可能的。关于此,我确信已发现了一种美妙的证
“将一个立方数分成两个立方数之和,或一个四次幂分成两个四次幂之和,或者一般地将一个高于二次的幂分成两个同次幂之和,这是不可能的。关于此,我确信已发现了一种美妙的证法 ,可惜这里空白的地方太小,写不下。”

正是因为费马没有写下证明,而费马的其他猜想却又对数学界贡献十分之多。许多的数学家在看到费马的一句话之后,都对其起了兴趣。包括数学界的泰斗欧拉,以及哥德巴赫等。将这个猜想换算成通俗语言,意思就是:

就以上这简简单单的一句话,无数的天才数学家都在为其神魂颠倒。1770年的时候,欧拉证明了费马猜想在N=3的时候成立,并将研究的成果发表在了自己的《代数指南》上面。其证明的方法是:
“无限下降法”和形如 数系的唯一因子分解定理”

但这仅仅只是一个小点,关于定理的终结还是遥遥无期。甚至1816年的时候,法国皇帝拿破仑都被他吸引。在拿破仑支持下的巴黎科学院于这一年设下了巨额的悬赏金,用以表彰那些能够解决这个数学难题的科学家。

通过这个理论,他一下子就证明了100以内除开39、59以及67之外所有的奇数在费马大定理上都成立,这是自研究费马大定理以来第一次重大的突破。但是在这之后,费马大定理的突破就停滞不前,甚至一度让数学界对其灰心丧气。

这位实业家曾在年轻的时候为情所困,一度到了想要自杀的时刻。但是就在自杀之前,他无意中读到了库默尔的“理想素数”理论。并通过这个看到了费马大定理,这个数学的爱好者不禁为其着迷并情不自禁地一直计算到天明。

自此之后,每年在世界上都会有成千上万个人宣称自己证明了费马大定理。 虽说大部分人都只是碰个运气或者说是跟风的民科,但这样的浪潮终究是让数学界对其重燃了兴趣。
自这之后,费马大定理翻开了新的篇章。这时候,离费马大定理被证明就只差临门一脚了。而这临门一脚,也历经了近70年的时间,在1993年才被剑桥牛顿学院的学者安德鲁·怀尔斯踹开。

1994年的10月25日,这是个值得令数学界纪念的日子。因为在这一天,怀尔斯向世界数学界发送了自己的验证费马大定理的完整证明邮件,其中包括一篇长文《模型椭圆曲线和费马大定理》。
这一次,他的论文经受住了数学界长达一年的拷问。直到1995年,《数学年刊》的第141卷录用怀尔斯的论文,一切盖棺定论。至此,那数学王冠上桂冠的芬香——费马大定理的证明就这样,被安德鲁·怀尔斯独享了。
文章来源:《应用数学和力学》 网址: http://www.yysxhlx.cn/zonghexinwen/2021/0617/753.html